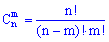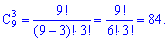Комбінаторика є важливим розділом математики, що досліджує закономірності розташування, впорядкування, вибору і розподілу елементів з фіксованої множини.
При великому числі можливих наслідків випробування способи прямого перебору можливих варіантів малоефективні. На допомогу приходять комбінаторні методи, в основі яких лежать два настутних правила.
ПРАВИЛО ДОДАВАННЯ
Якщо дві взаємовиключні події можуть бути виконані відповідно k та m способами, тоді якусь одну з цих подій можна виконати k+m способами.
Приклад 1. З міста А в місто В можна добратися 12 потягами, 3 літаками, 23 автобусами. Скількома способами можна добратися з міста А у місто В?
Розв'язання. Проїзд з А у В на потягу, літаку або автобусом є подіями, які не можуть виконуватися одночасно однією людиною (взаємовиключними), тому загальну кількість маршрутів можна обчислити сумуванням способів пересування
N=12+3+23=38.
В цьому і полягає правило додавання.
ПРАВИЛО МНОЖЕННЯ
Нехай дві виконувані одна за одною дії можуть бути здійснені відповідно k та m способами. Тоді обидві вони можуть бути виконані k*m способами.
Приклад 2. У турнірі беруть участь 8 команд з хокею. Скільки існує способів розподілити перше, друге та третє місця?
Розв'язання. Відповідно до умови аналіз призових місць має бути наступним:
перше місце займе одна з 8 команд, друге – одна з 7, третє – одна з 6, оскільки кожна з них не може претендувати одночасно на два призових місця. Тому таких способів буде
N=8*7*6=336
Обидва правила узагальнюються на випадок будь-якої скінченної кількості дій.
У комбінаториці розрізняють три види різних з'єднань (комбінацій) елементів фіксованої множини: перестановки, розміщення, сполучення. Нижче будуть дані їх означення з позначеннями, які найбільшвживані.
Перестановками з
m елементів називаються такі їх сукупності, що відрізняються одна від іншої тільки порядком входження елементів. Їх позначають
P(m) та визначають за формулою
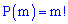

- факторіал числа
m, визначається за правилом
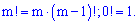
Приклад 3.Скількома способами можна в садочку поставити групу з 15 дітей в ряд?
Розв'язання. На перше місце є можливість поставити когось із 15 дітей, на друге одного з 14 і т.д. Загальна кількість рівна 15 факторіал
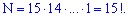
Переглянути
приклади на перестановки.
Розміщеннями з
n елементів по
m називаються такі сукупності
m елементів, що відрізняються одна від іншої принаймні одним елементом або порядком їх входження (
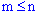
):
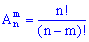
Фомула розміщень не надто складна і доволі часто Ви будете нею ористуватися на практиці, тому рекомендуємо її вивчити.
Приклад 4. Скільки різних трицифрових чисел можна скласти за допомогою цифр від 1 до 9?
Розв'язання Загальна кількість чисел обчислюється за формулою розміщень
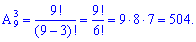
Отримана відповідь Вам і зрозуміла і тривіальна. Переглянути
задачі на розміщення.
Сполученнями з
n елементів по
m називаються такі сукупності
m елементів, що відрізняються одна від іншої принаймні одним елементом (
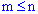
) :
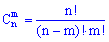
З формули сполучень бачимо, що вони приймають ще менше значення ніж розміщення. З наступного завдання Ви зрозумієте де використовують розміщення.
Приклад 5. Скількома способами можна вибрати три цифри з дев'яти 1, 2, 3,...,9?
Розв'язання. Кількість усіх можливих способів визначаємо з формули
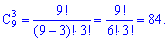

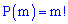
 - факторіал числа
- факторіал числа 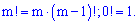
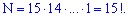
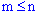 ):
):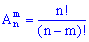
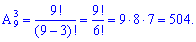
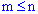 ) :
) :